熱線電話:0755-23712116
郵箱:contact@shuangyi-tech.com
地址:深圳市寶安區(qū)沙井街道后亭茅洲山工業(yè)園工業(yè)大廈全至科技創(chuàng)新園科創(chuàng)大廈2層2A

前面幾篇文章介紹的是圖像的空間域濾波,其對像素的處理都是基于像素的某一鄰域進行的。本文介紹的圖像的灰度變換則不同,其對像素的計算僅僅依賴于當前像素和灰度變換函數。
灰度變換也被稱為圖像的點運算(只針對圖像的某一像素點)是所有圖像處理技術中最簡單的技術,其變換形式如下:
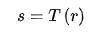
其中,T是灰度變換函數;r是變換前的灰度;s是變換后的像素。
圖像灰度變換的有以下作用:
? 改善圖像的質量,使圖像能夠顯示更多的細節(jié),提高圖像的對比度(對比度拉伸)
? 有選擇的突出圖像感興趣的特征或者抑制圖像中不需要的特征
? 可以有效的改變圖像的直方圖分布,使像素的分布更為均勻
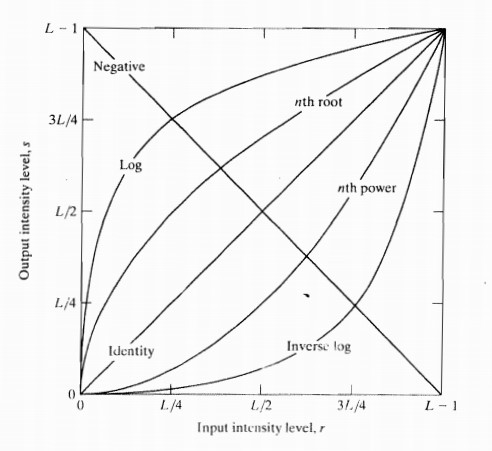
灰度變換函數描述了輸入灰度值和輸出灰度值之間變換關系,一旦灰度變換函數確定下來了,那么其輸出的灰度值也就確定了。可見灰度變換函數的性質就決定了灰度變換所能達到的效果。用于圖像灰度變換的函數主要有以下三種:
? 線性函數 (圖像反轉)
? 對數函數:對數和反對數變換
? 冪律函數:n次冪和n次開方變換
令r為變換前的灰度,s為變換后的灰度,則線性變換的函數:
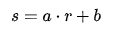
其中,a為直線的斜率,b為在y軸的截距。選擇不同的a,b值會有不同的效果:
?
?
?
?
?
?
在進行圖像增強時,上述的線性變換函數用的較多的就是圖像反轉了,根據上面的參數,圖像反轉的變換函數為:
圖像反轉的實現是比較簡單的,在OpenCV中有對Mat的運算符重載,可以直接Mat r = 255 - img或者~img來實現。
對數變換的通用公式是:
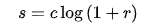
其中,c是一個常數,,假設
這使用的對數函數的底為10。由于灰度變換是灰度值之間的一對一的映射,而灰度值區(qū)間通常為[0,255],所以在進行灰度變換時,通常使用查表法。也就是,現將每個灰度值的映射后的結果計算出來,在變換時,通過查表得到變換后的灰度值。執(zhí)行上面結果得到的結果如下:
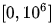 ,甚至更高。這樣范圍的值,顯示器是無法完整的顯示如此大范圍的灰度值的,因而許多灰度細節(jié)會被丟失掉。而將得到的頻譜值進行對數變換,可以將其動態(tài)范圍變換到一個合適區(qū)間,這樣就能夠顯示更多的細節(jié)。
,甚至更高。這樣范圍的值,顯示器是無法完整的顯示如此大范圍的灰度值的,因而許多灰度細節(jié)會被丟失掉。而將得到的頻譜值進行對數變換,可以將其動態(tài)范圍變換到一個合適區(qū)間,這樣就能夠顯示更多的細節(jié)。伽馬變換的公式為:
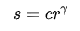
其中c和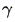 為正常數。
為正常數。
伽馬變換的效果與對數變換有點類似,當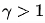
當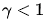
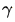 的值越小,對圖像低灰度值的擴展越明顯;當
的值越小,對圖像低灰度值的擴展越明顯;當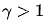
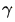 的值越大,對圖像高灰度值部分的擴展越明顯。這樣就能夠顯示更多的圖像的低灰度或者高灰度細節(jié)。
的值越大,對圖像高灰度值部分的擴展越明顯。這樣就能夠顯示更多的圖像的低灰度或者高灰度細節(jié)。
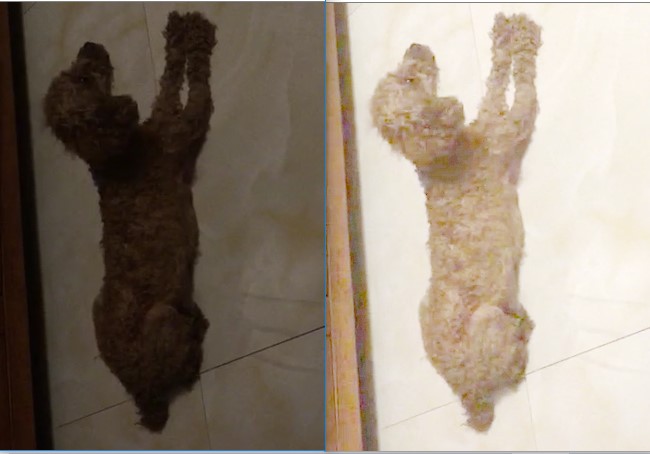
伽馬變換主要用于圖像的校正,對灰度值過高(圖像過亮)或者過低(圖像過暗)的圖像進行修正,增加圖像的對比度,從而改善圖像的顯示效果。
基于OpenCV的實現:
float pixels[256];
for (int i = 0; i < 256; i++)
pixels[i] = i * i *i;
Mat imageLog(image.size(), CV_32FC3);
for (int i = 0; i<image.rows; i++)
{
for (int j = 0; j<image.cols; j++)
{
imageLog.at
這里選擇的參數為c = 1,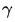

當選擇參數為c = 1,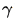

根據以上的結果,結合伽馬變換的函數曲線圖,做如下總結:
? 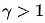
 的灰度區(qū)域映射到為
的灰度區(qū)域映射到為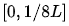 的輸出;而將
的輸出;而將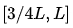 這部分高灰度區(qū)域映射到
這部分高灰度區(qū)域映射到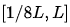 區(qū)間。這樣變換的結果就是,低于K的灰度區(qū)域被壓縮到更低灰度區(qū)間,而較亮的高灰度區(qū)域的灰度值被擴展到較大的灰度區(qū)間變的不那么亮,整體的效果就是圖像的對比度增加了,但是由于亮度區(qū)域被擴展,也就不那么亮了。
區(qū)間。這樣變換的結果就是,低于K的灰度區(qū)域被壓縮到更低灰度區(qū)間,而較亮的高灰度區(qū)域的灰度值被擴展到較大的灰度區(qū)間變的不那么亮,整體的效果就是圖像的對比度增加了,但是由于亮度區(qū)域被擴展,也就不那么亮了。
? 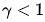
灰度變換屬于點對點的一一變換,在實現的時候,可以利用查表法。也就是實現將[0,255]區(qū)間的各個灰度值的變換后的值計算出來,在變換的時候直接根據灰度值進行查表得到變換后的結果。其實現如下:
/////////////////////////////////////////////////////////////////////
//
// 灰度線性變換函數
// 參數:
// src,輸入原圖像
// dst,輸出圖像,類型為CV_32F,大小及通道數與原圖像相同
// mapping,灰度映射表,可以根據不同的變換函數,提前計算好圖像的灰度映射表
//
////////////////////////////////////////////////////////////////////
void gray_trans(const Mat& src, Mat& dst,float* mapping)
{
int channels = src.channels();
if (channels == 1)
{
dst = Mat(src.size(), CV_32FC1);
for (int i = 0; i < src.rows; i++)
{
float* p1 = dst.ptr<float>(i);
const uchar* p2 = src.ptr(i);
for (int j = 0; j < src.cols; j++)
p1[j] = mapping[p2[j]];
}
}
else if (channels == 3)
{
dst = Mat(src.size(), CV_32FC3);
for (int i = 0; i < src.rows; i++)
{
float* p1 = dst.ptr<float>(i);
const uchar* p2 = src.ptr(i);
for (int j = 0; j < src.cols * 3; j+=3)
{
p1[j] = mapping[p2[j]];
p1[j+1] = mapping[p2[j+1]];
p1[j+2] = mapping[p2[j+2]];
}
}
}
} 其調用也比較簡單,根據具體的灰度變換函數,填充灰度映射表即可,以伽馬變換為例:
float pixels[256];
for (int i = 0; i < 256; i++)
pixels[i] = powf(i, 1.5);
Mat imageLog;
gray_trans(image, imageLog, pixels);本文主要對圖像的幾種常見的灰度變換進行了總結。
? 圖像反轉,是圖像線性變換的一種,可以得到圖像負片,能夠有效的增強圖像的暗色區(qū)域中的白色或者灰色細節(jié)
? 對數變換,擴展圖像中的低灰度區(qū)域,壓縮圖像中的高灰度區(qū)域,能夠增強圖像中的暗色區(qū)域的細節(jié);反對數變換與此相反。對數變換還有個重要作用是,能夠壓縮圖像灰度值的動態(tài)范圍,在傅立葉變換中能夠顯示更多的變換后的頻譜細節(jié)。
? 伽馬變換,主要用于圖像的校正,根據參數
文章轉自Brook_icv https://www.cnblogs.com/wangguchangqing/p/6983680.html